1. Fungsi Konstan
Fungsi Konstan bila setiap anggota A dipasangkan dengan satu anggota B yang sama
2. Fungsi Identitas
Fungsi Identitas bila setiap anggota domain dipasangkan dengan dirinya sendiri
3. Fungsi Linier
fungsi Linier diartikan dengan f(x)=ax+b. Grafiknya berupa garis lurus.
4. Fungsi Kuadrat
Fungsi Kuadrat diartikan dengan formula
f(x)=ax2+bx+c
Rumus titik puncak
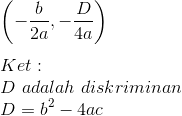
Rumus titik puncak
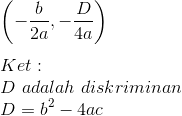
5. Fungsi Modulus / Fungsi Nilai Mutlak
Setiap fungsi f(x)= |x|, yang memasangkan bilangan real dengan nilai mutlaknya disebut fungsi modulus
6. Fungsi Tangga atau Fungsi Nilai Bilangan Bulat Terbesar
7. Fungsi Genap dan Fungsi Ganjil
Suatu fungsi y=f(x) disebut fungsi genap bila f(-x) = f(x)
Suatu fungsi y=f(x) disebut fungsi ganjil bila f(-x)= -f(x)















 About
About Tags
Tags Popular
Popular








